SIMULINK 3

Zawartość

Równanie Lotki-Volterry – dwa słowa wstępu. 1

Równanie Lotki-Volterry – dwa słowa wstępu

Równanie Lotki-Volterry lub inaczej równanie drapieżnik-ofiara, to nieliniowe równanie różniczkowe pierwszego stopnia. W literaturze można znaleźć kilka wersji tego modelu z różnymi uogólnieniami i udoskonaleniami, my jednak zajmiemy się podstawową wersją, dla łatwiejszej interpretacji wyników nie będziemy nawet zamieniali zmiennych na bezwymiarowe, co jest standardową procedurą przy rozwiązywaniu tego typu układów równań. Szczegółową analizę problemu można znaleźć choćby w książce J.D. Murraya: Wprowadzenie do Biomatematyki. Warszawa: PWN, 2006. ISBN 83-01-14719-9. Tu przedstawię tylko równania które można znaleźć np. na Wikipedii:

Gdzie:

x – populacja ofiar

y – populacja drapieżników

a - częstość narodzin ofiar lub współczynnik przyrostu ofiar,

b - częstość umierania ofiar na skutek drapieżnictwa,

c - częstość narodzin drapieżników lub współczynnik przyrostu drapieżników,

d - częstość umierania drapieżników lub współczynnik ubywania drapieżników

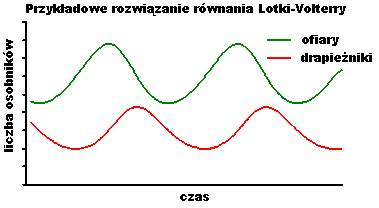
Rozwiązaniem tych równań przy odpowiednich warunkach początkowych są oscylujące w czasie liczby osobników dwóch kategorii:

Potrzebne elementy

Mając równania opisujące populacje ofiar i drapieżców mamy już w zasadzie wszystko co jest nam potrzebne do zbudowania modelu. Wystarczy teraz tylko skompletować potrzebne elementy, a są to odpowiednio:

· dwa Integratory – ponieważ mamy dwa wyrażenia do scałkowania

· dwa bloki Constans – odpowiadające stałym a i d

· dwa bloki Gain – odpowiadające stałym b i c

· dwa bloki Sum – do wykonania operacji dodawania i odejmowania w naszych równaniach

· dwa bloki Product – do wykonania mnożenia

· blok Scope i XY Graph – do wizualizacji wyniku

· blok Mux – do połączenia wejść do bloku Scope

Specjalnie pominąłem biblioteki gdzie można odnaleźć poszczególne bloki, ponieważ samodzielne ich odszukanie pozwoli na łatwiejsze zapamiętanie ich lokalizacji. Przygotowane elementy powinny wyglądać mniej więcej tak:

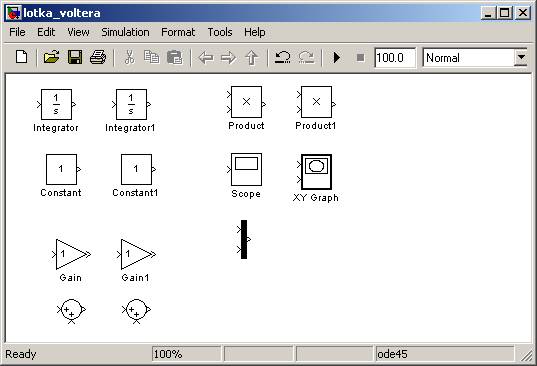
Pozostało tylko połączyć elementy w jedną całość i wpisać odpowiednie wartości parametrów a, b, c, d i wartości początkowych.

Kosmetyka 1

Zanim jednak Przejdziemy do połączenia elementów podpiszmy wybrane, aby ułatwić dalszą pracę. Zatem nazwijmy nasze Integratory literami x i y jako, że wynik całkowania daje nam właśnie wartości tych zmiennych w danej chwili czasu. Bloki Constant nazwijmy nazwami stałych a i d. Kolejne stałe kryją się pod blokami Gain – są to parametry b i c.

Łączenie elementów

Na początek proponuję połączyć wyjścia z bloków x i y z blokami b i c w celu pomnożenia ich przez odpowiednie stałe:

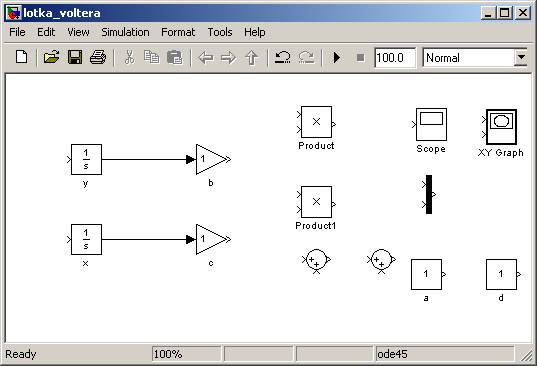
W kolejnym kroku dodajemy stałe a i d do odpowiednich iloczynów poprzez użycie bloków do sumowania Sum:

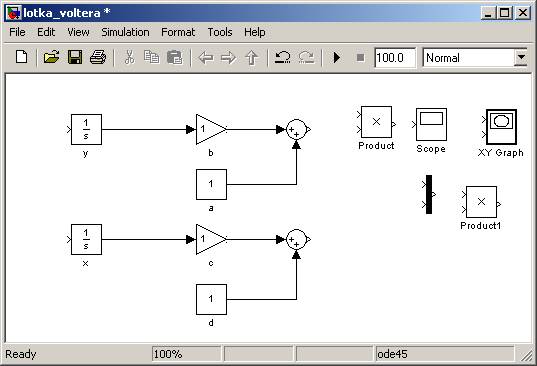
Wyniki sumowania musimy następnie pomnożyć przez odpowiednie wartości populacji, czyli x oraz y.

W tym celu użyjemy bloków Product. Wynik sumy łączymy z jednym wejściem tego bloku, a z drugiego wejścia „wyciągamy kabel” i „przylutowujemy” go do odpowiednich kabli wychodzących z Integratorów:

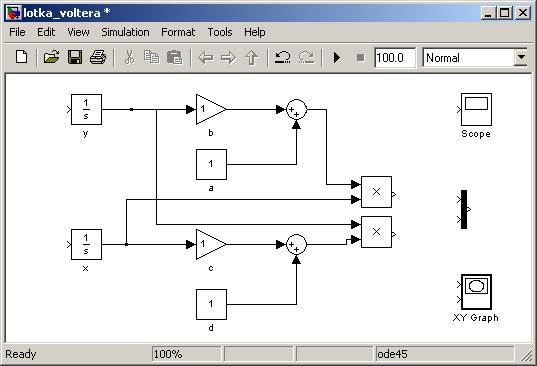
Teraz już możemy zamknąć nasz układ:

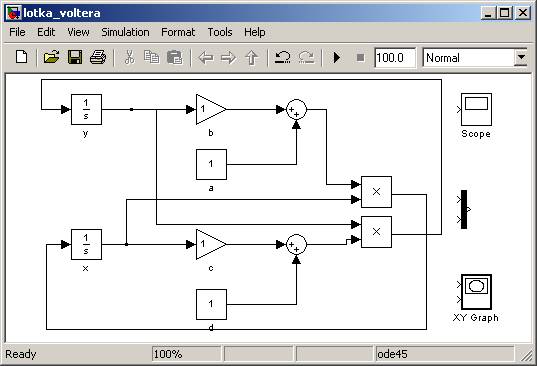
Ostatnim krokiem będzie dołączenie do obwodu bloków rysujących nasze rozwiązanie. Zaproponowałem dwa bloki, ponieważ na jednym przedstawimy oscylacje liczby osobników (blok Scope), a na drugim narysujemy portret fazowy. Blok Scope ma jedno wejście (możemy zwiększyć liczbę wejść wybierając w preferencjach liczbę osi, nie mniej my chcemy narysować wynik na jednej osi), dlatego też musimy użyć bloku Mux, aby połączyć wartości x i y w jeden wektor (macierz). Po dołączeniu tych bloków skończony model może wyglądać jak poniżej:

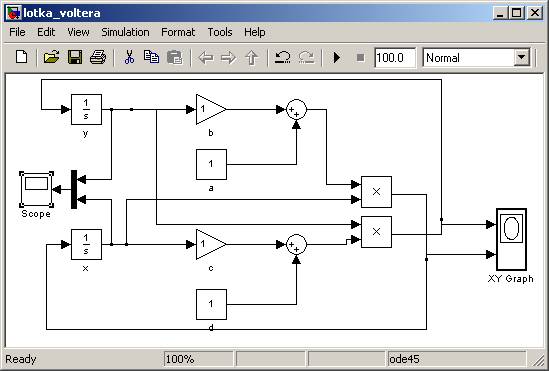
Jeśli uważnie się przyjrzymy schematowi, widzimy, że zaproponowany portret fazowy będzie zawierał pochodne liczebności populacji, a nie same liczebności.

Kosmetyka 2

Jeśli model wydaje się zbyt skomplikowany, proponuję zbudowanie dwóch podsystemów odpowiadających nawiasom w naszym wzorze wyjściowym. Takie bloki będą miały dwa wejścia i jedno wyjście:

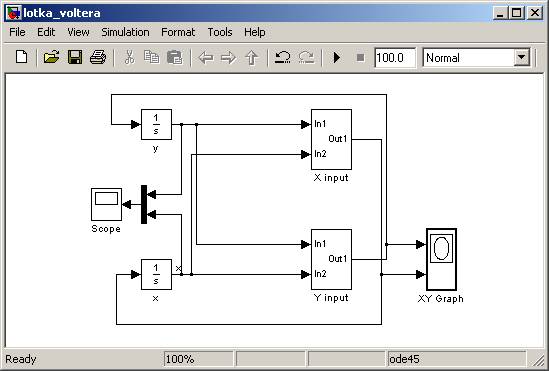
A podsystemy powinny wyglądać tak:

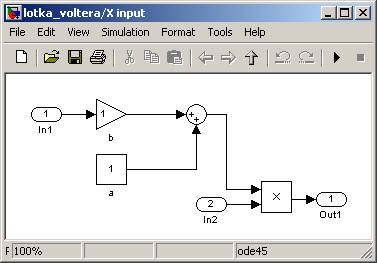
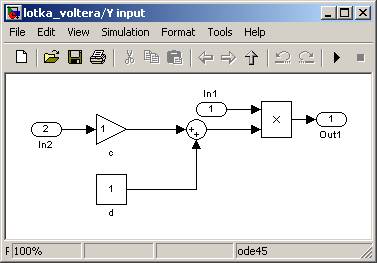
Jeśli ciężko jest nam zobaczyć które bloki są połączone za pomocą danego kabla, możemy wybrać z menu kontekstowego (klikając prawym przyciskiem myszy na konkretne połączenie) odpowiednie podświetlenie, np.:

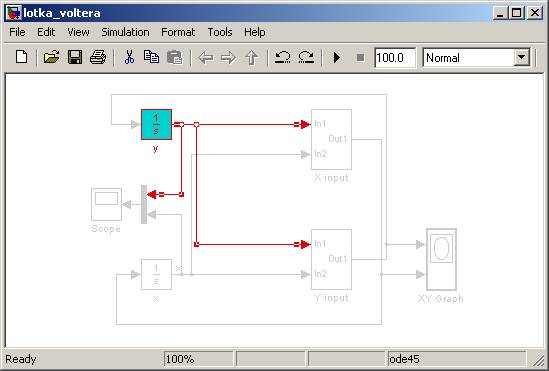
Podświetlenie usuwamy za pomocą opcji Remove Highlighting.

Symulacja

Nasz model jest już gotowy, zatem możemy przejść do jego testowania. Poniżej przedstawiam wyniki dla następujących parametrów wejściowych:

a = 1.2

b = 0.6

c = 0.3

d = 0.8

x(t=0) = 2

y(t=0) = 1

Należy pamiętać, że w naszym modelu używaliśmy tylko sumy, zatem aby wykonać potrzebne odejmowanie zmienne b i d musimy wpisać jako ujemne. Przed startem symulacji zmieńmy czas symulacji na 20, oraz Sample w bloku Scope na Sampling time = 0.01. Należy również poprawnie ustawić parametry bloku XY Graph na następujące: x-min=-2; x-max=3; y-min=-3.5; y-max=3; oraz sample time = 0.01;

Jesteśmy gotowi do symulacji, wyniki wyglądają następująco:

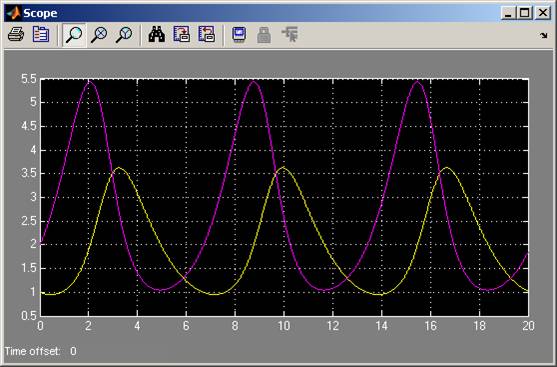
Która krzywa prezentuje drapieżników, a która ofiary ?

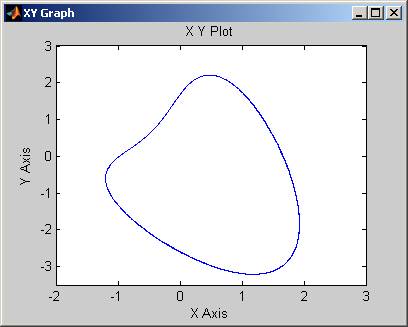
Teraz , możemy dowolnie manipulować parametrami. Jeśli np. ustawimy brak drapieżników na początku, to populacja ofiar będzie rosła wykładniczo do nieskończoności, co oczywiście nie jest prawdą, dlatego też wprowadza się poprawki do modelu np. na pojemność środowiska. Zachęcam zatem gorąco do rozbudowania tego modelu albo w stronę lepszego odwzorowania rzeczywistości, albo zwiększając liczbę rodzajów ofiar i drapieżników.

Do pobrania

· omawiany model

· Strona w formacie PDF

Spis wszystkich lekcji.

2010 – Grzegorz Knor