O środowisku

Simulink jest częścią pakietu matematycznego MATLAB firmy The MathWorks i służy do przeprowadzania symulacji komputerowych. Simulink pozwala budować modele symulacyjne przy pomocy interfejsu graficznego i tzw. bloków. Przy pomocy Simulinka można przeprowadzać zarówno symulacje z czasem dyskretnym jak i ciągłym.

Simulink znajduje głównie zastosowanie (poprzez to, że umożliwia symulacje w czasie ciągłym) w cyfrowym przetwarzaniu sygnałów, analizie obwodów elektrycznych i teorii sterowania

Uruchamianie

Aby uruchomić środowisko Simulink należy wpisać w command window Matlaba polecenie simulink lub kliknąć na pasku zadań ikonę programu:

W efekcie otworzy nam się główne okno programu Simulink Library Browser, gdzie możemy przeglądać dostępne biblioteki i zawarte w nich elementy.

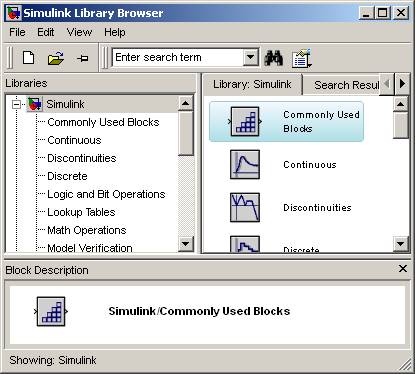
Idea tworzenia modeli

Simulinka możemy traktować jako nasze domowe laboratorium. Możemy sobie wyobrazić, że mamy do dyspozycji płytkę drukowaną do której możemy przylutować dowolny element, nieograniczoną liczbę kabli do łączenia płytek między sobą oraz do różnych urządzeń wejściowych i wyjściowych. Jedna różnica jest taka, że nie potrzebna nam lutownica, kalafonia i cyna tylko komputer z zainstalowanym środowiskiem Matlab&Simulink. Oczywiście porównanie to jak każda analogia ma swoje ograniczenia, ponieważ Simulink jest narzędziem o wiele potężniejszym. Za pomocą specjalnych bibliotek jego możliwości rosną. Możemy budować mechaniczne modele 3D za pomocą pakietu SimMechanics, możemy tworzyć oprogramowanie do rzeczywistych układów i wiele więcej. Nie mniej na tej stronie skupię się na opisie prostych modeli. A że moim zdaniem najbardziej efektywna nauka to tworzenie modeli, tworzenie i jeszcze raz tworzenie. Zatem przejdźmy do przykładów.

Pierwszy prosty model – figury Lissajou

Jeśli nie wiesz co to takiego figury Lissajou polecam artykuł na wikipedi: Krzywa Lissajous.

Żeby stworzyć nasz model w pierwszym kroku oczywiście uruchamiamy Simulinka z poziomu Matlaba. Następnie z menu File wybieramy New i New model lub szybciej klikając w odpowiednią ikonę na pasku menu bądź za pomocą skrótu Ctrl+N. Pojawi nam się puste okno modelu:

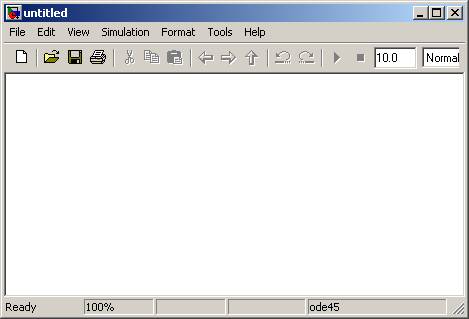
Do naszego prostego modelu potrzebne będą generatory sygnałów harmonicznych, czyli w najprostszym przypadku dwa sinusy. Znajdziemy je w bibliotece Simulink -> Sources. Przeciągamy dwukrotnie bloczek o nazwie Sine Wave do okna naszego modelu. Do konstrukcji naszego modelu potrzebny będzie jeszcze blok odpowiedzialny za wizualizację. Będziemy chcieli narysować krzywą, której współrzędne x będzie wyznaczał pierwszy generator sygnału, a współrzędne y drugi generator. Najlepiej do tego celu nadają się zwykłe osie, dokładnie takie same które pojawiają się po wywołaniu funkcji plot w Matlabie. Bloczek ten znajdziemy w bibliotece Simulink -> Sinks. Nazywa się XY Graph. Mamy zatem sytuację jak na poniższym rysunku rysunku:

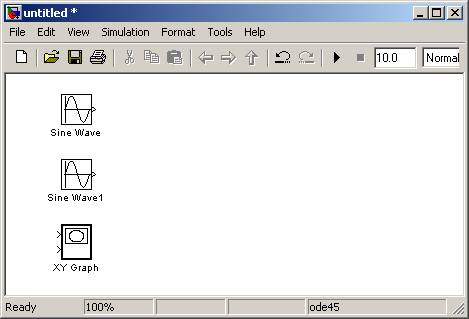
Nie pozostało nam teraz nic innego jak połączenie wszystkich elementów ze sobą. Oczywiście najpierw należy rozmieścić bloki tak, żeby wyglądało to względnie estetycznie. Jest to bardzo ważne, szczególnie przy bardziej skomplikowanych modelach, ponieważ poprawia to czytelność całego schematu ( o metodach zwiększających przejrzystość schematów będzie mowa w dalszej części). Łączyć elementy możemy na dwa sposoby. Pierwszy sposób poprzez kliknięcie na wyjście danego bloku |> i przeciągnięcie linii do wejścia >| innego bloku. Drugi sposób to kliknięcie bloku i następnie przytrzymując control kliknięcie drugiego bloku z którym ma być połączony. Kiedy połączymy wszystko zapisujemy nasz model. Modele tworzone w Simulinku mają rozszerzenie *.mdl.

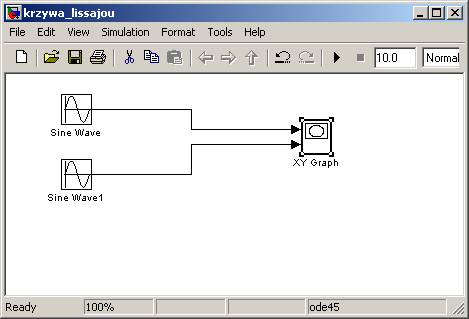
Właściwie nasz pierwszy model jest już gotowy. Możemy uruchomić symulację klikając guziczek play lub poprzez wybór z menu Simulation opcji start (dostępny jest również skrót klawiszowy Ctrl+T). Wynikiem będzie następujący wykres:

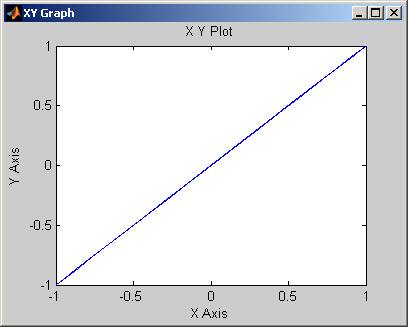
Należy przyznać, że nie są to takie ładne krzywe jak choćby te, które można obejrzeć na galerii Wikimedia Commons pod tym adresem: http://commons.wikimedia.org/..., a po drugie to dość skomplikowany sposób, żeby narysować prostą daną równaniem y=x. Aby otrzymać bardziej skomplikowane krzywe należy zmienić właściwości generatorów. Możemy to zrobić klikając dwukrotnie na blok Sine Wave lub Sine Wave1 w naszym modelu, otworzy się następujące okno preferencji:

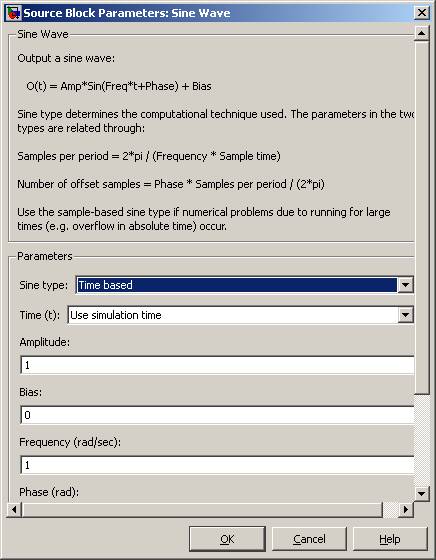
Manipulując częstościami i fazami obu bloków możemy dostać całą gamę krzywych Lissajou. Jeśli wydłużymy czas symulacji zmieniając jego wartość zaraz za guzikiem play będziemy mogli oglądać animację w oknie wykresu. Dla lepszego efektu wizualnego należy zmienić w preferencjach XY Graph wartość Sample time na jakąś małą np. 0.001. Przykładowa krzywa może wyglądać, tak jak poniżej:

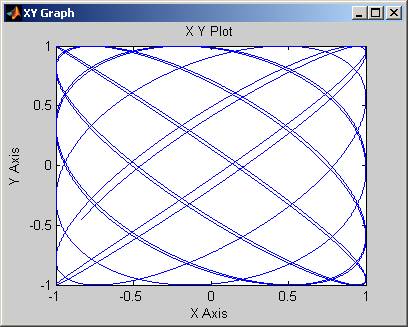
Na zakończenie proponuję poeksperymentować z wszystkimi możliwymi preferencjami dotyczącymi użytych bloków i z ustawieniami symulacji. Gdyby jakaś opcja nie była oczywista lub nieintuicyjna proszę o kontakt ze mną lub napisanie postu na forum matlaba.

Drugi prosty model – wahadło matematyczne

Kolejnym modelem będzie wahadło matematyczne. Utrudnienie będzie polegało nie tylko na większej liczbie elementów, ale na tym iż nasz model będzie rozwiązywał równanie różniczkowe. Do tego celu wykorzystywany jest tzw. Solver, który możemy wybrać w opcjach symulacji (lub po wybraniu skrótu Ctrl+E w oknie modelu). Na chwilę obecną nie musimy nic zmieniać w domyślnych opcjach, warto jednak wiedzieć, że mamy do wyboru kilka metod rozwiązywania równań. O wszystkich dostępnych opcjach możemy przeczytać w pomocy do programu: Solver Pane (pomoc jest również dostępna online).

Aby zamodelować wahadło matematyczne potrzebny jest nam wzór określający jego ruch. Wyprowadzenie wzoru można odnaleźć np. tutaj. A jego postać jest następująca:

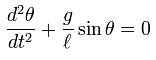
Gdzie θ to kąt wychylenia, a jego druga pochodna po czasie to przyspieszenie kątowe.

Pozostaje nam teraz wybrać bloki potrzebne do konstrukcji modelu. Będą to odpowiednio:

· Funkcja sinus: Trigonometric Function z biblioteki Math Operations

· Wzmocnienie reprezentujące wyraz g/l: Gain z biblioteki Math Operations

· Dwukrotne całkowanie: dwa bloki Integrator z biblioteki Continous

· Wykres wynikowy: np. blok Scope z biblioteki Sinks

Teraz pozostało połączenie wszystkich elementów w działającą całość. Zaczynamy od funkcji trygonometrycznej, którą zgodnie z naszym wzorem musimy pomnożyć (wzmocnić) przez współczynniki g/l ze znakiem minus (minus bierze się stąd, że rozwiązujemy równanie na przyśpieszenie kątowe które zgodnie z naszym wzorem wynosi –g/l sin θ). Łączymy ją zatem z blokiem Gain i ustalamy mu wartość np. -9.8, czyli zakładamy że długość naszego zamodelowanego wahadła wynosi 1m. Tak połączone bloki łączymy z pierwszym Integratorem. W wyniku pierwszego całkowania otrzymamy prędkość kątową. Następnie wyjście tego Integratora łączymy z kolejnym, aby otrzymać szukany kąt wychylenia θ. Czyli na wyjściu naszego drugiego Integratora mamy aktualną wartość kąta wychylenia, która stanowi podstawę do obliczenia tego kąta w kolejnym momencie czasu. Dlatego też wyjście drugiego Integratora jest argumentem wejściowym funkcji sinus. Otrzymaliśmy zatem zamknięty „obwód”, z którego chcielibyśmy móc zobaczyć wartość kąta wychylenia w danej chwili czasu. Posłuży nam do tego blok Scope. Aby „dolutować kabel” w dowolnym miejscu istniejącego obwodu należy nacisnąć lewym przyciskiem myszy na wejście do danego bloku >| i przeciągnąć do wybranego miejsca. Cały nasz model powinien wyglądać tak:

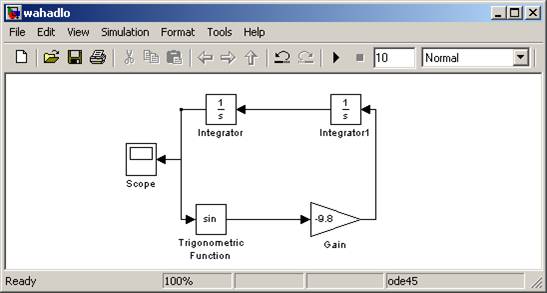
I tu pojawią się dwie rady dotyczące przejrzystości układu. Pierwsza rada: rozmiary dodanych elementów można dowolnie zmieniać klikając w wybrany blok i rozciągając go myszką, pozwoli to np. odkryć niewidoczne wartości wzmocnienia przy jego standardowej wielkości. Druga rada: aby obrócić dany blok wystarczy kliknąć na niego prawym przyciskiem myszki i z menu kontekstowego wybrać Format -> Flip block (lub za pomocą skrótu Ctrl+I).

Przed uruchomieniem naszej symulacji należy wybrać wartości początkowe prędkości (Integrator1) i położenia (Integrator). Po naciśnięciu przycisku play wynik możemy zobaczyć klikając dwukrotnie w blok Scope:

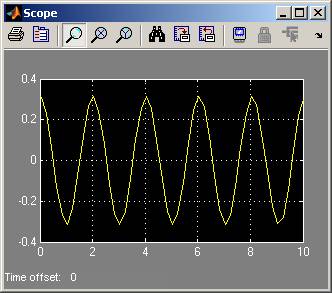
I na koniec oczywiście zachęcam do samodzielnego zbadania zachowania układu w zależności od wybranych parametrów i wyboru preferencji każdego z elementów. Pouczające będzie również wypróbowanie różnych Solverów.

A może teraz wahadło chaotyczne? :)

Spis wszystkich lekcji.

2010 – Grzegorz Knor